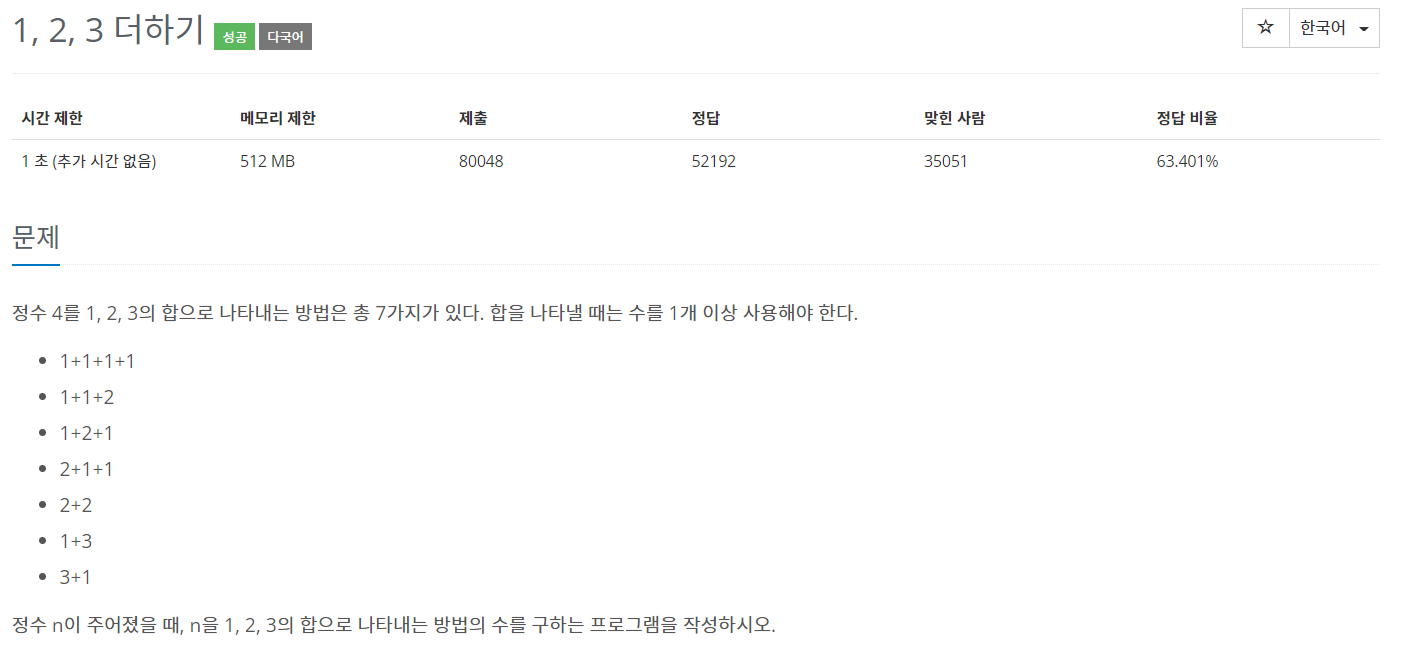

1, 2, 3 만으로 n을 만든다는 것 자체가 힌트였다.
우선 1, 2, 3을 사용해 1, 2, 3을 만들 수 있는 경우의 수가 필요하다.
왜냐하면 1,2,3 이후의 수,
예를 들어 4를 만들려면 이전의 수인 1, 2, 3에 3, 2, 1을 더해서 만들어야 하는데
1을 만들 수 있는 경우의 수 -> (1) : 1개
2를 만들 수 있는 경우의 수 -> (1,1), (2) : 2개
3을 만들 수 있는 경우의 수 -> (1,1,1), (1,2), (2,1), (3) : 4개
여기에 각각 3, 2, 1을 더하기만 하면 4가 되니
1, 2, 3을 이용해 4를 만들 수 있는 경우의 수는
이전의 수인 1, 2, 3를 만드는 경우의 수 그 각각의 합이 되는 것이다.
마찬가지로 5도 이전의 수인 4, 3, 2에 +1, +2, +3을 해서 만들 수 있기 때문에
4, 3, 2를 만드는 경우의 수를 더하면 그것이 5를 만드는 경우의 수가 되는 것이다.
이러한 규칙이 있으니 이제 코드를 짜면 된다.
1. 테스트케이스의 개수 T를 입력받는다.
2. 입력되는 수는 11보다 작다고 했으니 크기가 11인 int배열 dp를 생성한다.
3. 테스트케이스의 개수 T를 입력받는다.
4. 가장 기초 재료가 되는 1, 2, 3을 만들 수 있는 경우의 수를 배열의 값으로 초기화해준다.
5. 4부터 10까지 반복문을 사용해 인덱스값을 1, 2, 3의 합으로 표현할 수 있는 개수를 구해둔다.
(DP에서는 이미 해결한 서브 문제를 다시 구하지 않고,
그 값을 재활용한다)
6. T번 반복문을 돌며 N을 입력받고, dp[N]을 출력한다.
import java.io.*;
public class Main{
public static void main(String[] args)throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
int[] dp = new int[11];
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
for(int i=4;i<dp.length;i++){
dp[i] = dp[i-1]+dp[i-2]+dp[i-3];
}
for(int i=0;i<T;i++){
int N = Integer.parseInt(br.readLine());
System.out.println(dp[N]);
}
}
}
하아 어렵다
문제 자체가 어려운 게 아니라 문제를 보고 코드를 도출해내는 게 어렵다...
'Algorithm > [BOJ] - JAVA' 카테고리의 다른 글
| [백준] 11726 : 2xn 타일링 JAVA 풀이 (0) | 2022.06.08 |
|---|---|
| [백준] 2579 : 계단 오르기 JAVA 풀이 (0) | 2022.06.08 |
| [백준] 2748 : 피보나치 수 2 JAVA 풀이 (0) | 2022.06.07 |
| [백준] 2193 : 이친수 JAVA 풀이 (0) | 2022.06.07 |
| [백준] 1463 : 1로 만들기 JAVA 풀이 (0) | 2022.06.07 |



