
https://st-lab.tistory.com/255
[백준] 6549번 : 히스토그램에서 가장 큰 직사각형 - JAVA [자바]
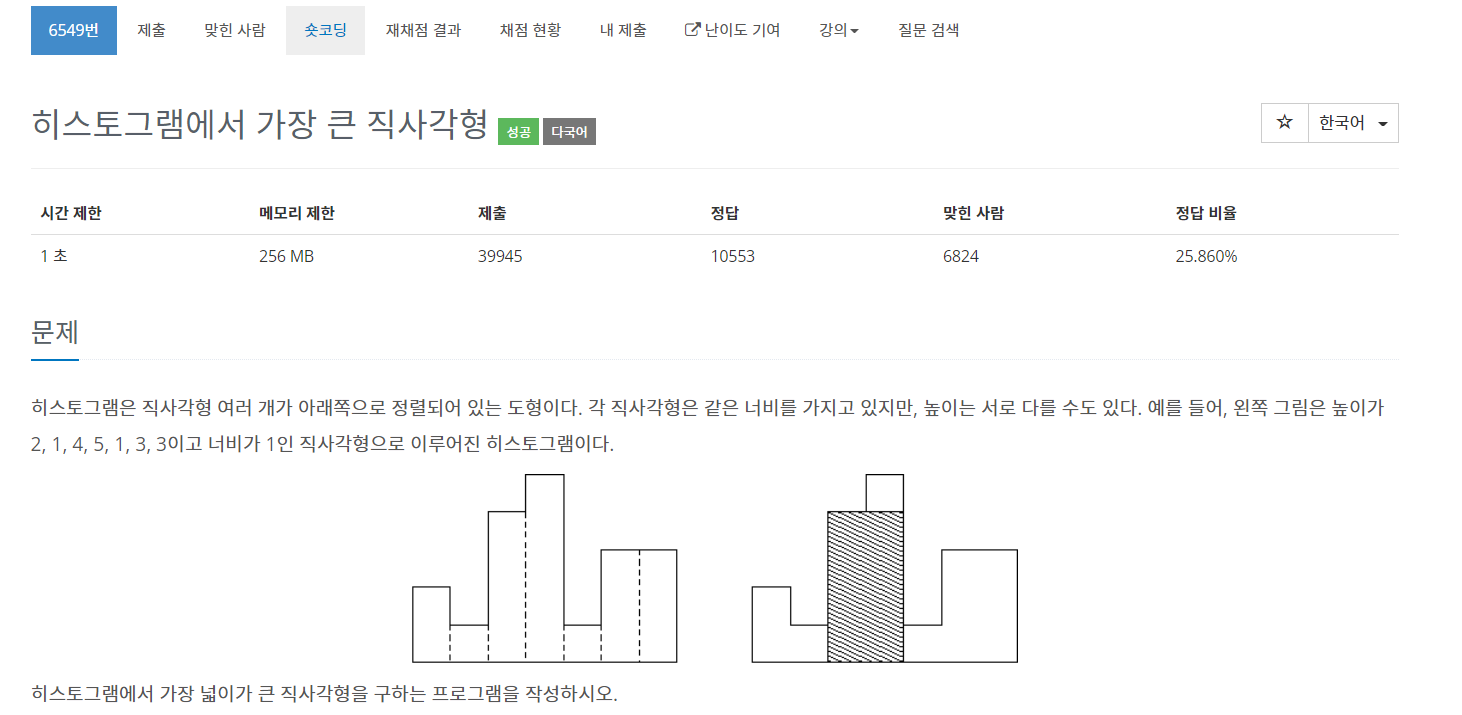
https://www.acmicpc.net/problem/6549 6549번: 히스토그램에서 가장 큰 직사각형 입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음
st-lab.tistory.com
이 포스트를 참고해서 풀었다.
import java.io.*;
import java.util.*;
public class Main {
static long[] histogram;
public static void main(String[] args)throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
String str = new String();
while(true) {
// 각 테스트케이스가 n과 n개의 숫자들로 입력되니 StringTokenizer로 값을 분리함
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
// 하나의 테스트케이스의 직사각형 개수를 n에 저장함
int n = Integer.parseInt(st.nextToken());
// 0이 입력되면 입력을 종료함
if(n==0) {
break;
}
// 직사각형 n개의 높이를 저장할 배열을 생성함
histogram = new long[n];
// 배열에 직사각형의 높이를 저장함
for(int i=0;i<n;i++) {
histogram[i] = Long.parseLong(st.nextToken());
}
// 가장 큰 직사각형의 넓이를 getArea함수를 실행해서 구하고,
// 그 값과 줄바꿈문자를 스트링빌더에 추가함
sb.append(getArea(0, n-1)).append('\n');
// 다음 테스트케이스를 위해 직사각형의 높이 배열을 초기화함
histogram = null;
}
// 스트링빌더에 저장된 내용을 출력함
System.out.println(sb);
}
// 가장 큰 직사각형의 넓이를 구하는 함수
public static long getArea(int low, int high) {
// 너비가 1이라면 그 사각형의 높이가 곧 넓이임
if(low==high) {
return histogram[low];
}
// 히스토그램을 분할하는 기준점이 될 중간값을 계산함
int mid = (low+high)/2;
// low부터 mid까지의 최대넓이
long leftArea = getArea(low, mid);
// mid+1부터 high까지의 최대넓이
long rightArea = getArea(mid+1, high);
// low ~ mid, mid+1 ~ high에서 각각 구한 직사각형의 넓이 중
// 더 큰 값을 max에 저장함
long max = Math.max(leftArea, rightArea);
// low ~ mid와 mid+1 ~ high 각각에서 구한 직사각형의 최대 넓이보다
// low ~ high 즉 쪼개지지 않은
// 히스토그램에서 더 큰 직사각형이 있을 수도 있으므로 아래 문장을 실행함
max = Math.max(max, getMidArea(low, high, mid));
// 가장 큰 직사각형의 넓이를 반환
return max;
}
// 쪼개지지 않은 히스토그램에서 더 넓은 직사각형이 있을 수도 있으므로
// 이를 확인하기 위한 함수를 생성
public static long getMidArea(int low, int high, int mid) {
// 왼쪽으로 넓혀나갈 변수
int toLeft = mid;
// 오른쪽으로 넓혀나갈 변수
int toRight = mid;
// 높이의 초기값
long height = histogram[mid];
// 넓이의 초기값
long maxArea = height;
// 히스토그램의 범위를 넘어가지 않는 한 반복
while(low < toLeft && high > toRight) {
// 왼쪽보다 오른쪽의 높이가 더 높을 경우
if(histogram[toLeft-1]<histogram[toRight+1]) {
// 사각형을 오른쪽으로 확장
toRight++;
// 높이는 기존 높이와 오른쪽 사각형의 높이 중 더 낮은 것으로 갱신함
// 그렇게 하지 않으면 직사각형이 히스토그램을 벗어나게 될 수도 있기 때문
height = Math.min(height, histogram[toRight]);
}
// 오른쪽보다 왼쪽의 높이가 더 높을 경우
else {
// 사각형을 왼쪽으로 확장
toLeft--;
// 마찬가지고 기존 높이와
// 왼쪽 사각형의 높이 중 더 낮은 것으로 높이를 갱싱함
height = Math.min(height, histogram[toLeft]);
}
// 기존 최대넓이와 새로운 직사각형의 넓이 중 더 큰 것으로 갱신
maxArea = Math.max(maxArea, height*(toRight-toLeft+1));
}
// 히스토그램의 오른쪽끝까지 탐색이 끝나지 않았다면
while(high>toRight) {
// 오른쪽으로 이동하고 높이 갱신 후 최대 넓이를 계산
toRight++;
height = Math.min(height, histogram[toRight]);
maxArea = Math.max(maxArea, height*(toRight-toLeft+1));
}
// 히스토그램의 왼쪽끝까지 탐색이 끝나지 않았다면
while(low<toLeft) {
// 왼쪽으로 이동하고 높이 갱신 후 최대 넓이를 계산
toLeft--;
height = Math.min(height, histogram[toLeft]);
maxArea = Math.max(maxArea, height*(toRight-toLeft+1));
}
// 최대 넓이를 반환함
return maxArea;
}
}'Algorithm > [BOJ] - JAVA' 카테고리의 다른 글
| [백준] 2740 : 행렬 곱셈 JAVA 풀이 (0) | 2022.09.16 |
|---|---|
| [백준] 2261 : 가장 가까운 두 점 JAVA 풀이 (0) | 2022.09.16 |
| [백준] 2630 : 색종이 만들기 JAVA 풀이 (0) | 2022.09.13 |
| [백준] 1517 : 버블소트 JAVA 풀이 (0) | 2022.09.12 |
| [백준] 2448 : 별 찍기 - 11 JAVA 풀이 (0) | 2022.09.12 |



